Résumé
Les teintes utilisées dans les enluminures varient au cours du temps et suivant le lieu de production. Nous nous sommes donc interrogés sur la possibilité d’une mesure de distance entre enluminures reposant sur les teintes, qui reflète la proximité temporelle et géographique des enluminures. A travers cet article nous étudions différentes mesures et nous montrons la pertinence de ces mesures à travers la réalisation d’un jeu de test reposant sur un échantillon de manuscrits. Nous proposons une visualisation tridimensionnelle des distances mesurées, afin de vérifier la constitution de groupes dans l’espace correspondant à des enluminures de même origine.
Abstract
Colors used in middle ages illuminations vary depending on the time and place of painting. In this paper we focus on image distance measurements that reflect this proximity of time and place across various illuminations. We present a nearest neighbor test conducted over a set of illuminations, which highlights the relevance of the distance measurements. We also propose a 3D visualization of these distances, in order to check that groups formed in this space correspond to coherent sets of illuminations in terms of time and place of painting.
Sommaire
Introduction
L’étude présentée dans cet article s’inscrit dans le cadre de l’Action Concertée Incitative « Formes et Couleurs », et part du constat que, suivant les époques et les lieux de réalisation, les pigments, et donc les teintes, utilisés pour les enluminures, varient. Nous avons cherché à vérifier ce constat de manière numérique. L’objectif de cette étude est de proposer et évaluer des outils informatiques reposant sur la couleur et pouvant aider le médiéviste à dater un document (ou du moins les enluminures de ce document), détecter des anomalies, proposer une date pour une enluminure non classée, etc. Pour ce faire, nous avons implanté deux mesures de distance inter-enluminures reposant sur les couleurs, puis nous avons étudié la corrélation entre la distance mesurée entre deux enluminures et la proximité géographique et temporelle de celles-ci.
Dans cet article nous présentons d’abord les mesures de distance utilisées ainsi que les notions sous-jacentes (espace colorimétrique, histogramme de couleurs). Nous présentons ensuite les mesures réalisées sur un échantillon d’enluminures numérisées, et nous évaluons leur pertinence par le biais d’une recherche de plus proche voisin. Nous introduisons ensuite un outil de visualisation développé par notre équipe, offrant une vue synthétique des distances entre enluminures et aidant par conséquent à valider graphiquement les mesures de distance proposées. Nous concluons enfin sur un tour d’horizon des perspectives ouvertes par cette étude.
Mesure de distances inter-enluminures
Notion d’espace colorimétrique
Nos mesures de distance inter-enluminures reposent sur la notion d’espace colorimétrique [Kowaliski 1999]. Un espace colorimétrique est un espace à plusieurs dimensions (en général trois) dont chaque coordonnée définit une teinte. La littérature définit trois grandes catégories d’espaces colorimétriques, reposant respectivement sur une approche purement visuelle (espaces perceptuels), purement physique (espaces dépendants du matériel), ou physique corrigée par des données psychométriques (espaces de référence). L’approche purement visuelle classe les couleurs par proximité visuelle. De par sa nature intuitive, elle est assez souvent utilisée dans le traitement numérique des couleurs. On peut par exemple citer l’espace TSL (teinte, saturation, luminosité). L’approche purement physique décrit les couleurs à partir de composantes correspondant au périphérique utilisé. L’espace RVB (rouge, vert, bleu) constitue un exemple très connu de ce type d’espace. Il permet de définir les couleurs par rapport aux trois canaux rouge, vert et bleu dont dispose la plupart des dispositifs d’affichage (écrans d’ordinateurs, etc.). Les espaces de référence, tels L*a*b ou Luv, ressemblent aux espaces perceptuels dans la mesure où les teintes s’y décomposent en une luminosité (L) et deux composantes de « couleur » à proprement parler (teinte et saturation). Ces espaces présentent toutefois la particularité de refléter les distances entre couleurs perçues par l’œil humain de manière uniforme.
Histogramme tridimensionnel
Il est possible, dans un but d’analyse, de représenter une image par son histogramme de couleurs [Chuan 1996], c’est-à-dire de considérer un ensemble de teintes et d’indiquer pour chacune de ces teintes le nombre de pixels de l’image qui lui correspond. Afin de comparer les enluminures, nous avons choisi de les représenter par un histogramme tridimensionnel. En d’autres termes nous utilisons une matrice tridimensionnelle dont chaque dimension correspond à une dimension de l’espace colorimétrique utilisé. Chaque élément de cette matrice contient le nombre de pixels de l’image dont la teinte correspond aux coordonnées de cet élément. Par exemple, si la matrice M représente l’histogramme d’une image dans l’espace RVB, et si l’élément M[10,20,30] vaut 35, cela signifie que l’image contient 35 pixels de teinte (R=10,V=20, B=30).
Nous avons apporté quelques adaptations à cet histogramme. Tout d’abord, nous limitons le nombre de teintes considérées. L’espace RVB définit en général 256 niveaux de rouge, de vert et de bleu, ce qui devrait conduire à une matrice de taille 256×256×256, assez lourde à manipuler. Nous considérons donc un nombre de niveaux réduit, typiquement 16 niveaux pour chaque canal. Ceci permet également d’atténuer les effets de dégradés en regroupant des pixels de teintes voisines. D’autre part, suivant la mesure effectuée, nous utiliserons soit un histogramme de présence soit un histogramme de fréquence de couleur. Dans l’histogramme de présence, noté P, nous considérons que P[i,j,k] vaut 1 si M[i,j,k] > 0 (l’image contient au moins un pixel de cette teinte), et 0 sinon. Dans l’histogramme de fréquence, noté F, chaque valeur ne correspond pas à un nombre de pixels d’une teinte donnée, mais au pourcentage des pixels de l’image correspondant à cette teinte. Ceci permet de traiter indifféremment des images de taille différente.
Distance inter-matrices
La littérature propose un grand nombre de méthodes de calcul de distance inter-images [Stricker 1994 ; Smith 1996 ; Aslandogan 1999 ; Rui 1999 ; Goldberger 2002]. Dans l’ensemble, l’objectif de ces méthodes consiste à retrouver des images similaires en terme de contenu. Dans notre cas, nous utilisons ces méthodes afin de retrouver des images similaires en termes de palette. En conséquence nous avons volontairement laissé de côté les méthodes qui tiennent compte de la localisation des teintes dans l’image.
Nous avons choisi d’utiliser deux approches simples reposant sur les couleurs communes aux deux images. Dans un premier cas nous comptons uniquement la proportion de couleurs communes, et dans le second cas nous considérons la fréquence des couleurs.
Distance fondée sur la proportion de couleurs communes
Soit I1 et I2 les deux images à comparer. Soit P1 et P2 les histogrammes de fréquence représentant respectivement I1 et I2. Soit card(P) la taille d’un histogramme. Appelons dc1 la première mesure de distance, reposant sur le nombre de couleurs communes. Si nbc, nb1 et nb2 représentent respectivement le nombre de couleurs en commun, le nombre de couleurs présentes dans P1 et le nombre de couleurs présentes dans P2, nous posons :
dc1(P1,P2) = ((nb1+nb2-nbc) / nbc) – 1 si nbc > 0, et dc1(P1,P2)= card(P) si nbc=0.
Ainsi, la distance est proportionnelle au nombre de couleurs présentes dans l’une ou l’autre image, divisé par le nombre de couleurs communes. Pour deux images identiques, on a nb1=nb2=nbc, donc dc1=0. Afin de gérer le cas où deux images ne possèdent pas de couleurs communes, nous posons une distance maximum card(P) justifiée comme suit : la plus grande valeur de dc1 observable, lorsqu’il existe au moins une couleur commune, correspond au cas où une seule couleur est commune alors que chaque couleur est présente dans l’une ou l’autre matrice. Dans ce cas nb1+nb2=card(P)+1, et ((nb1+nb2-nbc) / nbc) = (card(P)+1-1)/1 = card(P). On peut donc raisonnablement poser dc1(P1,P2)= card(P) si nbc=0.
Distance fondée sur la fréquence des couleurs
La seconde mesure utilisée repose sur la présence des couleurs et leur fréquence dans les deux images [Swain 1991]. On calcule la distance dc2 comme étant la somme des différences de fréquences pour chaque teinte entre les deux histogrammes de fréquence :
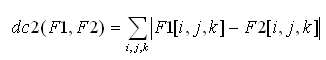
Pour deux images identiques, la distance minimum est bien égale à zéro. Pour deux images différentes, elle est positive et augmente avec la dispersion. On peut noter que la valeur maximale de dc2 est 200 %. Elle correspond au cas où il n’y a pas de couleur commune entre les deux histogrammes. En conséquence pour chaque coordonnée i,j,k nous avons au moins l’une des deux valeurs F1(i,j,k) ou F2(i,j,k) qui est nulle, d’où :
Les deux mesures dc1 et dc2 considèrent chaque teinte indépendamment de ses voisines. Ceci implique qu’avec des matrices de trop grande dimension, des teintes voisines, résultant possiblement d’un effet de dégradé, seront considérées comme totalement différentes. D’où l’intérêt de réduire la taille de la matrice. Par ailleurs, cette indépendance limite l’influence de l’espace colorimétrique retenu. Nous avons donc considéré qu’il n’était pas nécessaire d’avoir recours à un espace de référence et nous avons utilisé l’espace RVB.
Au vu des résultats des tests que nous présentons dans les sections suivantes, nous n’avons pas jugé nécessaire, pour l’instant, de rechercher des mesures de distance plus performantes. Une investigation plus approfondie des mesures de distance fera l’objet de travaux ultérieurs.
Discussion sur la notion de distance
Nous avons jusque-là considéré que dc1 et dc2 constituaient des mesures de distance entre enluminures, ce qui, du point de vue de la définition d’une distance, s’avère inexact. Une distance présente les quatre propriétés de minimalité, de symétrie, d’identité et d’inégalité triangulaire.
La propriété de minimalité indique que la distance d’une enluminure à elle-même est nulle. Cette propriété est bien vérifiée pour dc1 et dc2. La propriété de symétrie indique que, pour deux enluminures quelconques e1 et e2, d(e1,e2)=d(e2,e1). Cette propriété est bien vérifiée pour dc1 et dc2. L’identité est vérifiée si pour deux enluminures quelconques e1 et e2, d(e1,e2)=0 si et seulement si e1=e2. Nos deux mesures ne vérifient pas cette propriété pour les enluminures. En revanche, elles la vérifient respectivement pour les histogrammes de présence et de fréquence.
L’inégalité triangulaire est vérifiée si, pour trois enluminures quelconques e1, e2 et e3, d(e1,e2)+d(e2,e3)>= d(e1,e3). dc2 vérifie cette propriété. En réalité dc2 est par définition une distance, car il s’agit d’une distance de Manhattan mesurée dans une partie de l’espace Rn*n*n (c’est-à-dire un espace dont chaque dimension correspond à un élément de l’histogramme, en considérant que l’on dispose de n niveaux de rouge, de vert et de bleu). En revanche, cette propriété n’est pas vérifiée par dc1. Il convient donc de considérer dc1 non pas comme une distance mais plutôt comme une mesure de dissimilarité.
En conclusion, dc1 constitue une mesure de dissimilarité entre les histogrammes de présence de couleurs dans les enluminures, et dc2 constitue une mesure de distance entre les histogrammes de fréquence de couleurs dans les enluminures.
Tests
Description du jeu de test
Les tests présentés dans cet article reposent sur des enluminures provenant des fonds numérisés de la Bibliothèque Mazarine et de la Bibliothèque municipale de Valenciennes. La plupart de ces enluminures sont consultables en ligne via le site Liber Floridus (http://liberfloridus.cines.fr) en ce qui concerne la Bibliothèque Mazarine et le site Enluminures (http://www.enluminures.culture.fr) pour la Bibliothèque municipale de Valenciennes. Nous avons utilisé une base de 198 enluminures numérisées provenant de 15 manuscrits. Ces images sont majoritairement originaires de France (Paris, Nord, Est, Sud-Ouest). Leur datation s’échelonne du xiie au xve siècle. Le tableau 1 donne une vue synthétique de ces informations.
| Cote Manuscrit | Bibliothèque | Région | Époque | Nombre d’enluminures utilisées |
|---|---|---|---|---|
| M0001 | Mazarine | France – Sud-Ouest | Début xiie siècle | 18 |
| M0003 | Mazarine | France - Est | Début xiie siècle | 17 |
| M0004 | Mazarine | France - Est | Début xiie siècle | 18 |
| M0008 | Mazarine | France | Second quart xiiie siècle | 11 |
| M0009 | Mazarine | France | Troisième quart xiiie siècle | 18 |
| M0011 | Mazarine | France | Troisième quart xiiie siècle | 12 |
| M0012 | Mazarine | France – Paris | Début xiiie siècle | 18 |
| M0013 | Mazarine | France ? Nord ? | Fin xiiie siècle | 19 |
| M0469 | Mazarine | Paris / Angleterre | xve siècle | 21 |
| M3469 | Mazarine | France - Paris | Fin xiiie siècle | 14 |
| V0001 | Valenciennes | France - Nord | Troisième quart xiie siècle | 7 |
| V0002 | Valenciennes | France - Nord | Troisième quart xiie siècle | 5 |
| V0003 | Valenciennes | France - Nord | Troisième quart xiie siècle | 6 |
| V0004 | Valenciennes | France - Nord | Troisième quart xiie siècle | 5 |
| V0005 | Valenciennes | France - Nord | Troisième quart xiie siècle | 9 |
Les numéros indiqués correspondent aux cotes des manuscrits dans leurs bibliothèques respectives. Afin de distinguer les deux sources nous avons fait précéder le numéro de référence d’un M. (Mazarine) ou d’un V (Valenciennes). Les images utilisées sont le résultat d’une numérisation calibrée, ce qui assure une relative stabilité des teintes à travers les différentes images. Les images d’origine sont souvent cadrées assez large et laissent donc apparaître, outre l’enluminure, une surface importante de support et de texte. Afin de limiter l’influence de ces derniers lors de nos mesures, nous avons recadré manuellement les images numérisées, l’efficacité de ce recadrage dépendant toutefois de la forme de l’enluminure. Il convient de noter qu’à plus grande échelle un recadrage automatique serait nécessaire.
Mesures réalisées
Afin de tester l’adéquation et la pertinence des mesures de distance proposées, nous avons réalisé un test de plus proche voisin : pour chaque enluminure Ei, on recherche l’enluminure Ej la plus proche vis-à-vis de la mesure de distance considérée, puis on vérifie si elles appartiennent bien au même manuscrit. Dans un premier temps nous avons volontairement retenu ce dernier critère afin de rendre le test plus contraignant. En effet, l’appartenance à un même manuscrit va au-delà de la proximité chronologique ou géographique.
Le tableau 2 présente une synthèse des calculs de plus proche voisin réalisés sur les 15 manuscrits à l’aide des mesures dc1 (couleurs communes) et dc2 (fréquences). Ce tableau indique pour chaque manuscrit le nombre d’erreurs de classement observées, ainsi que la liste (et la proportion) des manuscrits dans lesquels ont été fait ces classements défectueux. Par exemple, nous pouvons observer que pour la mesure dc1, cinq enluminures du manuscrit M0003 ont été classées par erreur dans le manuscrit M0004.
| Manuscrit | Nb. enlum. | Nb. Erreurs (dc1) | Classements défectueux avec dc1 (manuscrit et quantité) |
Nb. erreurs (dc2) | Classements défectueux avec dc2 (manuscrit et quantité) |
|---|---|---|---|---|---|
| M0001 | 18 | 0 | - | 0 | - |
| M0003 | 17 | 5 | M0004(5) | 4 | M0004(4) |
| M0004 | 18 | 10 | M0003(8), M0001(1), M0012(1) | 6 | M0003(5),M0001(1) |
| M0008 | 11 | 1 | M0001(1) | 5 | M0013(2),M0004(1),M0009(1),M0012(1) |
| M0009 | 18 | 0 | - | 2 | M0013(2) |
| M0011 | 12 | 1 | M0013(1) | 1 | M0013(1) |
| M0012 | 18 | 1 | M0009(1) | 3 | M0011(2),V0005(1) |
| M0013 | 19 | 0 | - | 2 | M0008(1),M0009(1) |
| M0469 | 21 | 0 | - | 0 | - |
| M3469 | 14 | 0 | - | 0 | - |
| V0001 | 7 | 3(0) | V0002(2),V0004(1) | 2(0) | V0002(1),V0005(1) |
| V0002 | 5 | 2(0) | V0001(1),V0004(1) | 3(0) | V0001(3) |
| V0003 | 6 | 3(0) | V0004(2),V0005(1) | 1(0) | V0004(1) |
| V0004 | 5 | 5(0) | V0005(2),V0001(1),V00002(1),V0003(1) | 5(0) | V0002(3),V0001(1),V0005(1) |
| V0005 | 9 | 3 (0) | V0001(1),V0003(1),V0004(1) | 4(0) | V0001(3),V0003(1) |
Nous pouvons constater le classement parfait des enluminures provenant des manuscrits M0001, M0469, M3469 avec les deux mesures de distance. La mesure dc2 génère plus d’erreurs sur l’ensemble du jeu d’essai, mais la mesure dc1 accentue les cas de confusion les plus forts, entre les manuscrits M0003 et M0004. Les deux manuscrits M0003 et M0004 provenant de la même région et de la même époque, nous pouvons raisonnablement penser que cette confusion n’en est pas vraiment une. Quelques erreurs résiduelles peuvent s’expliquer par le fait d’ajouts de pages dans des manuscrits anciens. C’est par exemple le cas pour le début du manuscrit M0004, qui est un ajout provenant d’un manuscrit daté du xiiie ou xive siècle, et dont l’origine présumée est l’Est de la France. L’image correspondante a été classée avec le manuscrit M0012 (France – Paris, début xiiie). Ce classement n’est probablement pas exact, mais il est par contre logique que cette enluminure ne soit pas classée avec le reste du manuscrit M0004 (France Est, début xiie).
Concernant les manuscrits provenant de la Bibliothèque de Valenciennes, il s’agit de cinq volumes d’une même bible. En conséquence, les erreurs apparentes sont encore une fois liées au critère de bon classement (même manuscrit). Dès lors que le critère de bon classement considère les manuscrits de même origine, nous pouvons constater que le taux d’erreur tombe à 0 pour ces cinq volumes (chiffres entre parenthèses dans la colonne « nombre d’erreurs »).
Si nous tenons compte de l’origine commune des manuscrits de la Bibliothèque municipale de Valenciennes, le taux de bon classement s’élève à 91 % pour dc1, et à 88 % pour dc2. Si nous considérons de plus que M0003 et M0004 sont de même origine, ce taux monte à 95 % pour dc1 et 93 % pour dc2. Les deux mesures s’avèrent donc très efficaces et pertinentes sur ce jeu d’essai. La mesure dc1 reposant sur la proportion de couleurs communes est ici la plus performante. Celle reposant sur les fréquences fournit également de bons résultats, mais commet d’avantage d’erreurs de classement.
Visualisation
Nous développons actuellement, au sein de notre équipe de recherche en apprentissage, un outil de visualisation spatiale. Cet outil permet de visualiser des informations sous la forme de points dans des espaces à deux ou trois dimensions. Plusieurs objectifs sont recherchés à travers un tel outil. Tout d’abord, comprendre et mettre en œuvre différentes techniques de représentation spatiale. Ensuite, adapter ces techniques à différentes méthodes d’apprentissage, par exemple à la classification automatique. Enfin, permettre la recherche et l’implantation de méthodes d’interaction à plusieurs niveaux dans le processus d’apprentissage (visualisation directe de l’influence du paramétrage, interaction graphique dans les critères de classification, etc.).
Principe de visualisation
Entre autres fonctionnalités, notre outil permet de visualiser des distances dans l’espace. Nous avons pour cela eu recours au positionnement multidimensionnel (ou MDS – Multi Dimensional Scaling) [Kruskal 1978 ; Cox 2000]. Cette approche permet de placer des points dans l’espace à partir des distances connues entre ces points. Ce placement n’est trivial que lorsque les distances fournies en entrée correspondent à des distances euclidiennes. Si ce n’est pas le cas, le positionnement multidimensionnel permet de rechercher un espace de projection des points qui limite les distorsions, c’est-à-dire dans lequel la somme des erreurs entre les distances fournies et observées est la plus faible. Pour cet espace de projection on peut choisir un nombre de dimensions quelconque. Nous utilisons dans notre outil des espaces à deux ou trois dimensions. L’approche que nous avons retenue pour le positionnement multidimensionnel consiste à faire l’hypothèse qu’il existe une représentation des objets dans un espace euclidien (de dimension éventuellement grande) dans lequel les distances entre points correspondent aux distances entre les objets fournis. Dans ce cas, le MDS est équivalent à une analyse en composantes principales (c’est-à-dire à une réduction du nombre de dimensions afin de ne conserver que les dimensions les plus significatives). Il est d’ailleurs à noter que, outre le positionnement multidimensionnel, notre outil permet également d’utiliser l’analyse en composantes principales ; nous ne servons pas toutefois de cette fonctionnalité dans le cadre des distances inter-enluminures.
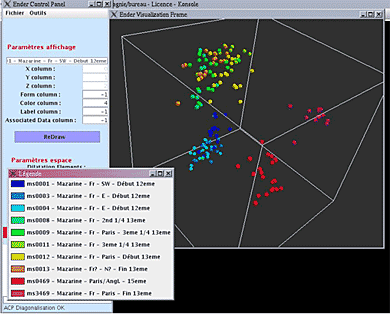
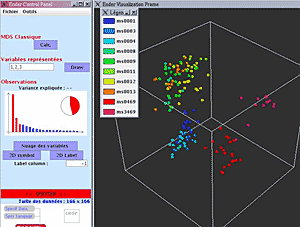
La figure 1 donne une vue d’ensemble du logiciel de visualisation. Cette capture d’écran présente une visualisation des distances dc2 entre les enluminures extraites des manuscrits de la Bibliothèque Mazarine. Nous pouvons constater que les enluminures se regroupent bien par époque et par origine. La légende aide ici à identifier les groupes hétérogènes comme étant composés d’enluminures de même époque et de même origine géographique.
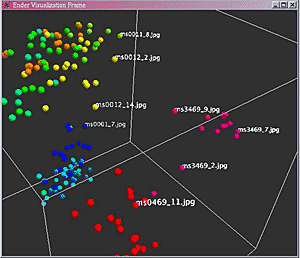
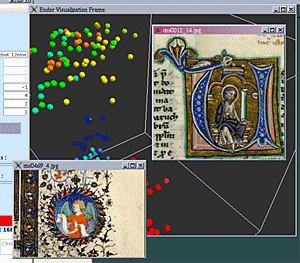
Afin de rendre la visualisation plus agréable, il est également possible de faire varier la taille des points ainsi que leur espacement. Il est naturellement possible de faire pivoter l’espace de représentation et de s’y déplacer suivant les différents axes (gauche/droite, haut/bas, avant/arrière). Il est aussi possible d’associer une étiquette (par exemple, le nom du fichier image associé) à chaque point [figure 2], d’aller puiser des informations fournies dans les fichiers de données, tels les groupes d’appartenance des points (afin de constituer la légende), les fichiers associés aux points (afin, par exemple, de visualiser l’enluminure correspondant à un point donné, figure 3), et de jouer sur la forme des points suivant la valeur d’un critère (sphères, cônes, etc.).
Il est enfin possible d’utiliser une fonction de zoom, c’est-à-dire de sélectionner un sous-ensemble de points et de les faire apparaître dans une seconde fenêtre, ce qui permet par exemple d’affiner la répartition spatiale d’un groupe et donc de faire potentiellement apparaître des sous-groupes.
Justification de l’outil de visualisation
La plupart des outils statistiques commercialisés proposent des interfaces de visualisation reposant en général sur l’analyse en composantes principales, parfois sur le positionnement multidimensionnel. Toutefois, nous n’avons pas connaissance d’outils comparables au nôtre. En général, les outils statistiques offrent une visualisation en deux dimensions, moins confortable à manipuler, notamment pour l’utilisateur non spécialiste. Par ailleurs, les différentes fonctionnalités que nous avons associées à la visualisation des points (zoom, fichier associé, etc.), ainsi que les possibilités d’extension (interfaçage avec les algorithmes d’apprentissage) nous semblent justifier pleinement l’originalité et l’apport de cet outil.
Visualisation des différentes mesures de distance
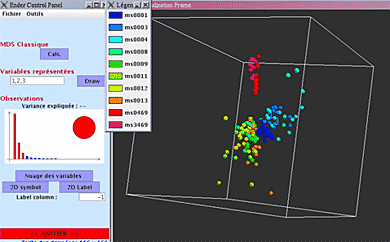
Les deux copies d’écran suivantes illustrent la représentation spatiale calculée par l’algorithme MDS pour nos deux mesures de distance. Afin de rendre ces images plus lisibles, nous n’avons fait apparaître que les manuscrits de la Bibliothèque Mazarine. La figure 4 présente la distribution pour la mesure dc1 (nombre de couleurs communes). La figure 5 correspond à la mesure dc2 (fréquence des couleurs). Nous pouvons constater que visuellement la mesure la plus intéressante semble être dc2, car elle diffuse assez bien les points dans l’espace, tout en préservant des groupes homogènes. La mesure dc1 génère des groupes plus compacts, comme nous avons pu le pressentir lors du calcul des plus proches voisins, mais certains groupes sont très proches visuellement alors qu’ils sont d’époques différentes (par exemple ms 0469 et ms 3469).
Il convient également d’attirer l’attention sur la variance expliquée, c’est-à-dire sur la distorsion entre distances mesurées et distances visualisées. Cette information apparaît dans la fenêtre de contrôle de l’outil sous formes de barres verticales. Chaque barre indique la variance expliquée par une dimension (c’est-à-dire l’intérêt de chaque dimension dans la représentation des distances fournies en entrée), les barres rouges indiquant les dimensions utilisées pour la visualisation. Nous pouvons constater que la distorsion est nettement plus faible avec dc1. Notre approche du positionnement multidimensionnel repose sur l’hypothèse qu’il existe un espace de grande dimension dans lequel la distance entre points correspond à la distance entre objets. Or pour dc1 il est probable que cet espace n’existe pas, puisque dc1 ne constitue pas une distance. En conséquence, la représentation graphique obtenue, ainsi que la variance expliquée, sont probablement faussées. D’autres approches du positionnement multidimensionnel pourraient résoudre ce problème.
Conclusion et perspectives
Les travaux présentés dans cet article s’articulent autour de deux axes : la mesure de distances ou de dissimilarité entre des histogrammes de couleurs représentant des enluminures, et la visualisation spatiale de ces mesures. Nous avons évalué la pertinence des mesures proposées grâce à une approche numérique (recherche des plus proches voisins). Celle-ci a révélé que dans l’ensemble les distances mesurées sont plus faibles entre enluminures de même source qu’entre enluminures de sources différentes. Ceci nous conduit donc à penser que les couleurs des enluminures constituent une notion discriminante, et que les mesures utilisées s’avèrent appropriées. Si le calcul du plus proche voisin fournit un résultat synthétique, nous avons pu constater que l’utilisation de méthodes de visualisation en général, et de notre outil en particulier, offrent un gain de compréhension non négligeable, permettant d’appréhender en un seul regard l’ensemble des distances mesurées, et d’apprécier la cohérence des groupes d’enluminures.
Si la mesure reposant sur la proportion de couleurs communes s’est avérée plus performante pour le calcul du plus proche voisin, nous avons en revanche remarqué que la mesure de distance issue à partir des fréquences était plus agréable à utiliser dans la phase de visualisation. Ceci nous conduit à penser que pour notre problème, et sans doute dans un cadre beaucoup plus général, différents types de mesures (distance, dissimilarité, etc.) peuvent être utilisées suivant le post-traitement effectué.
Sur le plan technique, on peut s’interroger sur la validité de tests reposant uniquement sur la numérisation d’enluminures anciennes. Les teintes ont pu se modifier au cours du temps, du fait des pigments et du support utilisés. De plus la numérisation peut ne pas toujours refléter la perception naturelle des teintes (par exemple pour les zones dorées). Bien entendu, une analyse chimique des pigments s’avérerait certainement plus fiable que la simple analyse des images numérisées. Toutefois, celle-ci suppose la mise en œuvre de moyens nettement plus lourds que ceux que nous avons employés. Naturellement, il pourrait être intéressant de mettre en œuvre les deux approches afin d’évaluer leur complémentarité.
L’avenir de nos travaux consiste d’une part à affiner les mesures de distances et d’autre part à développer de nouvelles fonctionnalités de visualisation. Concernant les mesures de distances, il conviendrait de conduire des tests sur un nombre nettement plus important d’enluminures. Le test de plus proche voisin devrait alors obligatoirement tenir compte de la proximité géographique et temporelle, et non plus du seul manuscrit. Il pourrait également être intéressant, pour des raisons de performances, de mettre en œuvre des mesures utilisant des informations plus synthétiques que la matrice de présence et/ou de fréquence des teintes. Nous cherchons notamment à définir pour chaque enluminure une liste limitée de couleurs représentatives, et à faire porter la mesure de distance sur ces dernières. Il existe déjà une grande variété de techniques allant en ce sens [Heckbert 1982 ; Smith 1996 ; Boughorbel 2002], et nous travaillons actuellement à un algorithme reposant sur l’approche EM (expectation maximisation) [Dempster 1977] utilisant un mélange de lois statistiques pour décrire la répartition des couleurs dans l’histogramme.
Les fonctionnalités de visualisation que nous prévoyons d’implanter dans l’avenir suivent plusieurs directions. Du point de vue visuel, nous cherchons à améliorer la séparation entre paquets de points. Nous prévoyons également de pouvoir injecter « à la volée » de nouveaux points correspondant à des enluminures d’origine inconnue ou contestée, et d’observer leur placement afin d’aider le médiéviste dans le processus de localisation spatiale et/ou temporelle. Enfin, comme pour le test de plus proche voisin, la représentation simultanée d’une grand nombre de points ouvre différentes voies, que ce soit du point de vue de la capacité d’affichage (mémoire utilisée et taille d’écran, utilisation de dispositifs de réalité virtuelle) ou de la lisibilité des données (effet de zoom sur les groupes, masquage partiel, etc.).